忙しい人のためのmatplotlibのAxes3Dのbar3d関数の引数の設定方法のメモ。

最終更新日: Sat Nov 21 23:09:29 2020 +0900

はじめに

この記事で3次元の棒グラフを作ってみましたが、この形で表示するためにかなり手間取ってしまいました。

手間取ったポイントは多岐にわたりますが、本記事ではその中でも最もサクッと忘れてしまうものと考えられる「3次元の棒グラフを描くための関数(mpl_toolkits.mplot3d.axes3d.Axes3Dクラスのbar3d関数、以下単に『bar3d関数』と書きます。)」の引数の設定の方法について書きます。

基本的な考え方

3次元の棒グラフは変数$x$,$y$に対応する位置に関数$z = f(x,y)$で表される値$z$を高さとする直方体を$x$,$y$の値をある値域の範囲内で変化させつつ多数描いたものであると考えることができます。

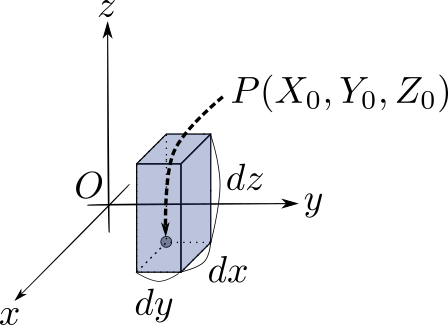
その多数描かれているであろう直方体のうち1本を取り出すと、以下のように図示できます。

bar3d関数では上図の$X_0, Y_0, Z_0, dx, dy, dz$を使って描画の位置を指定します。

なお、直方体の描画位置は複数になる(ことが一般的だと思われますが…)場合には原則として各直方体ごとに上記の各変数に対応する値を変数ごとにまとめて1次元の配列で指定します(一部例外があります。次節参照)。したがって、変数$x$,$y$がPython3のプログラムによる処理で2次元の配列になっている場合であっても、何らかの方法で1次元の配列に変換する必要があります。

例えば、直方体が3個(仮に$V_1,V_2,V_3$とします。)からなる棒グラフを描く場合には、$X_0$のかわりに$V_1$の$X_0$, $V_2$の$X_0$, $V_3$の$X_0$をこの順に並べたものを1次元の配列として指定します。

bar3d関数での引数の指定方法

bar3d関数で3次元の棒グラフを描くために必要な変数及びその設定の方法は以下の通りです。

指定が必須の変数

指定が必須の変数は以下の通りです。

$x$,$y$の値に対応する値$z=f(x,y)$を第6引数に設定する必要があるのが、少々わかりにくいところです。

第1引数: xy平面に平行な長方形の頂点のうちのx座標(2個)のうちの1個を指定します。前節の$X_0$に相当する値になります。第4引数にも負の値が指定できるっぽいために遠回りな書き方になりますが、第4引数に正の値を指定する場合には、上記のx座標のうちの小さい方を指定します。
第2引数: xy平面に平行な長方形の頂点のうちのy座標(2個)のうちの1個を指定します。前節の$Y_0$に相当する値になります。第5引数にも負の値が指定できるっぽいために遠回りな書き方になりますが、第5引数に正の値を指定する場合には、上記のy座標のうちの小さい方を指定します。
第3引数: xy平面に平行な長方形の頂点のうちのz座標のうちの1個を指定します。前節の$Z_0$に相当する値になります。第6引数では直方体のz軸方向の長さを指定することになりますので、特殊な棒グラフを描くのでない限り0を指定します。
第4引数: 棒のx軸方向の(おそらく符号付きの)長さを指定します。前節の$dx$に相当する値になります。なお、負の値が実際に指定できるかどうかは未確認です。スカラ値を指定した場合には、棒グラフのすべての棒のx軸方向の長さが指定した値になります。
第5引数: 棒のy軸方向の(おそらく符号付きの)長さを指定します。前節の$dy$に相当する値になります。負の値が実際に指定できるかどうかは未確認です。スカラ値を指定した場合には、棒グラフのすべての棒のy軸方向の長さが指定した値になります。
第6引数: 棒のz軸方向の符号付きの長さを指定します。前節の$dz$に相当する値になります。負の値が実際に指定できるかどうかは未確認ですが、おそらく指定できます。

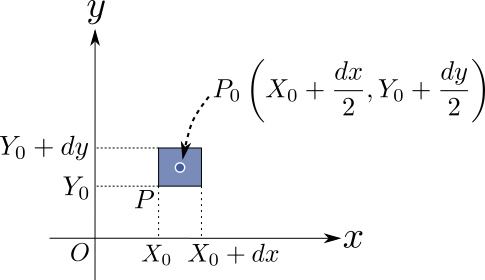
また、第1引数及び第2引数に指定される$x$, $y$はxy平面上においては格子状に配列されることが一般的であると考えられますが、その値をそのままbar3d関数の引数に指定すると、棒グラフを構成する直方体の頂点の$x$座標及び$y$座標の値がそれぞれ$x$,$x+dx$のどちらか一方及び$y$,$y+dy$のどちらか一方の組み合わせになりますので、棒グラフの面のうちxy平面に平行な長方形の中心の座標は$(x+\displaystyle\frac{dx}{2},y+\displaystyle\frac{dy}{2})$となります。

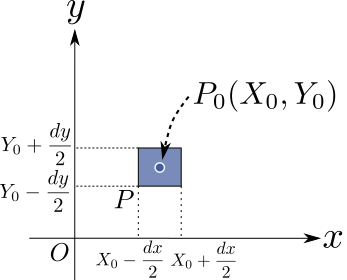
一般に棒グラフの高さによって示される値は変数$x$, $y$に対応する統計量と考えられますので、棒グラフを構成する直方体の頂点の$x$座標及び$y$座標の値がそれぞれ$x-\displaystyle\frac{dx}{2}$,$x+\displaystyle\frac{dx}{2}$のどちらか一方及び$y-\displaystyle\frac{dy}{2}$,$y+\displaystyle\frac{dy}{2}$のどちらか一方の組み合わせとなるように指定し、棒グラフの面のうちxy平面に平行な長方形の中心の座標が$(x,y)$となるようにします。

具体的にはbar3d関数の第1引数及び第2引数に$x-\displaystyle\frac{dx}{2}$及び$y-\displaystyle\frac{dy}{2}$をそれぞれ指定します。

# X,Yは長さnの1次元の配列とします。
dx = np.full_like(X,1)
dy = np.full_like(Y,1)
X0,Y0 = X-dx/2, Y-dy/2

配列の場合でも3行で書けてしまうので、楽チンです。

指定が必須でない(オプショナルな)変数

bar3d関数によって描かれる棒はカラーマップによって着色することができますが、matplotlibはいくつかのカラーマップをビルトインしています。それらのカラーマップはmatplotlib.pyplot.cmを通して利用することができます(matplotlib.pyplot.cmはmatplotlibからimportされたビルトインのカラーマップです)。

以下の手順でコードを書くことで、matplot3dで用意されているビルトインのカラーマップを使って棒を着色できます。なお、この記事ではカラーマップとして”terrain_r”というビルトインのカラーマップを使用しています。

データ値に対応するカラーマップの色を選択して表示するための正規化クラスのインスタンスを作成します(以下のコード例ではmatplotlib.pyplotがpltとしてimportされているものとします)。
```
norm = plt.Normalize(0,dz.max())
```
前項のnormは変数を指定して実行できますので、bar3d関数の第6引数と同じ変数(配列)を第1引数として代入して実行して正規化を行った配列を求め、さらにそれをカラーマップ(これはmatplotlibの内部においてlocals().update()関数を使って生成したカラーマップのインスタンスをcmのローカル変数に追加しているものです。)名に変数を指定して実行すると、各データに対応する色を得ることができます。
```
colors = plt.cm.terrain_r(norm(dz))
```
前項のcolorsをbar3d関数の引数に追加します。
カラーバーの作成及びグラフへの追加

単に棒グラフを着色しただけだと、色と対応する数値の関係が把握しにくいです。

そこで、以下のコードを追加してカラーバーの作成し、グラフへ追加がします。

colourMap = plt.cm.ScalarMappable(cmap=plt.cm.terrain_r)
colourMap.set_array(dz)
colBar = plt.colorbar(colourMap).set_label('z-value')

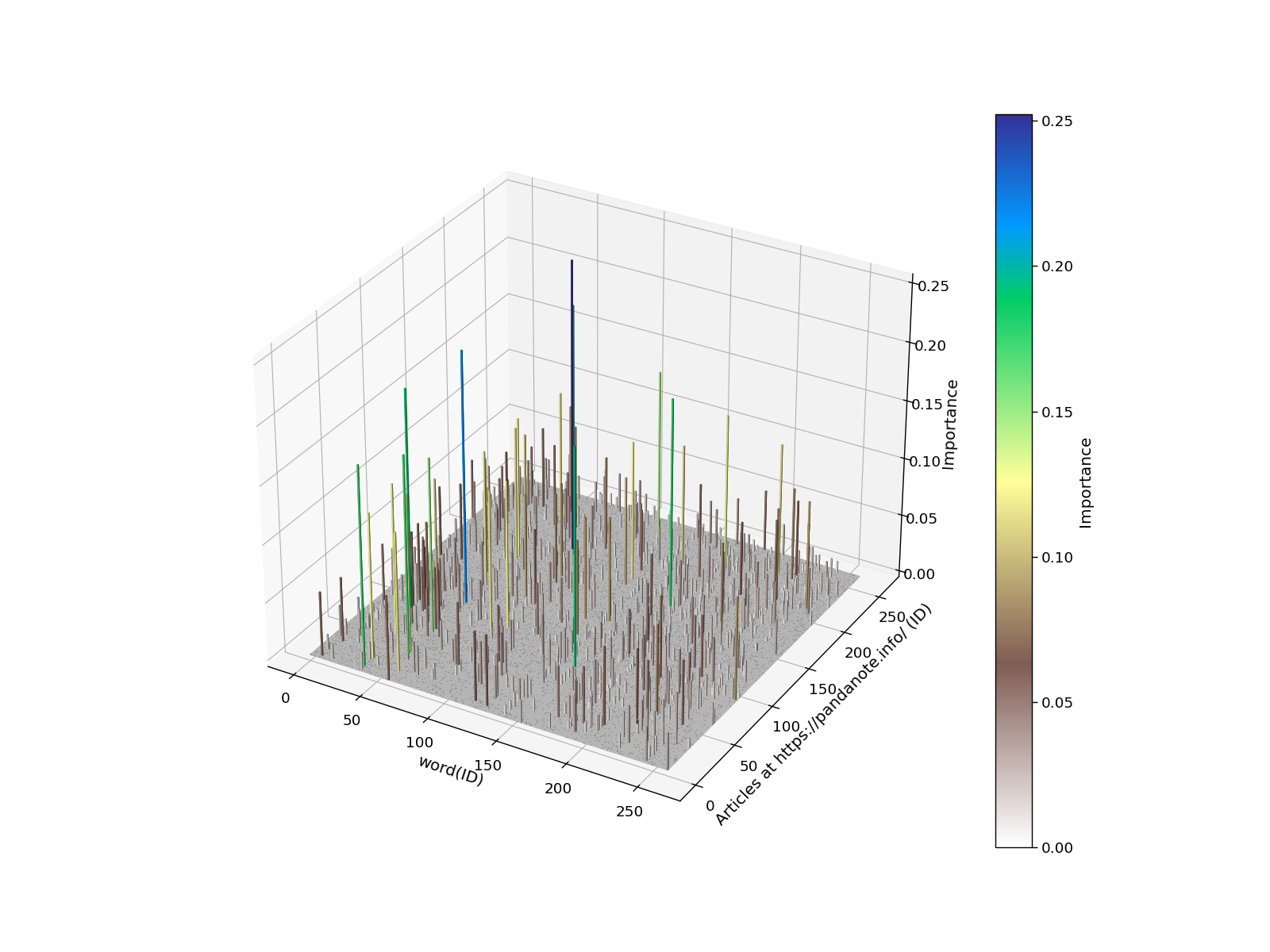
描画例

以下のような感じのグラフが出力できます。

まとめ

基本的な考え方はシンプルなものであり、3次元の直交座標系において描画に必要な点の指定の方法が理解できれば、描画処理(3次元→2次元への投影等)についてはmatplotlibにおまかせにできる分だけ直感的にわかりやすいものではあります。

しかし、おまかせにできるということはその部分はブラックボックスになるということも意味しますし、「棒グラフを構成する『棒』の『底面』の長方形の中心座標がいい感じになるように指定する方法。」のような感じの微妙に曖昧な覚え方をしてしまうと後でほぼ確実にわからなくなってしまうと思ったので、メモ書きとして記述することとしました。

この記事は以上です。

リンク

panda大学習帳外伝

勝利の方程式の解き方。