メインページ | panda大学習帳 | 第三倉庫(仮) | 用語集📒 | 本サイトについて | プライバシーポリシー
回らない複素積分。
この記事で、$\displaystyle\int_{0}^{\infty}\left(\displaystyle\frac{\sin x}{x}\right)^n dx$を部分積分と複素積分を駆使して計算しました。
上記の計算の際にいきなり複素積分を行わなかったのは、以下の理由によります。
- 積分経路として$n$位の極を経路によって囲まれる領域内に含まず、かつそれを避ける経路を設定していること。
- $n \gt 1$の場合には、「$n$位の極のまわりの半径$r$の小さな円を$\alpha(\gt 0)$周する経路に沿った複素積分の値はその円を1周した場合の$\alpha$倍になる」的な定理のようなものが成り立たないこと。
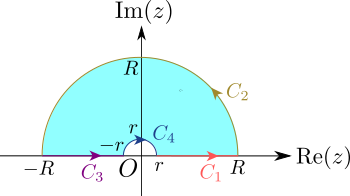
$n(\gt 1)$位の極をよけるような積分経路(下図の$C_4$に相当する経路です。)を考える際に、つい上記の後者のような計算をしたくなってしまいますが、これは一般的には成り立ちません。
そこで、部分積分などを駆使して被積分関数の分母の次数を下げるなどの工夫が必要になります。
スポンサーリンク
そのような工夫を行って計算を行った例が、この記事になるというわけです。
そこで、この記事ではそのような工夫をしないで計算をするとその計算結果がどうなるのかを考えることにします。
問題の設定。
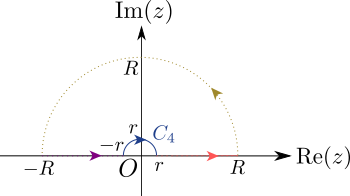
まず、複素平面上に$n(\gt 1)$位の極を持つ被積分関数を考えたうえで、積分の経路をかなり大幅に限定して、$n(\gt 1)$位の極のまわりの半径$r$小さな円のまわりを半周回る経路に沿った複素積分 \begin{align} I &= \int_{C_4} \frac{1}{z^n} dz\, (n \gt 1) \label{eq:intalongsemicirclearoundpole} \end{align} の値を計算してみることにします。
なお、(\ref{eq:intalongsemicirclearoundpole})式の積分の経路$C_4$は下図の青色の実線になります。
サクサクと計算。
問題の設定ができたら、サクサクと計算します。
例によって、$z = re^{i\theta}$とおくと、$dz = ire^{i\theta}d\theta$と形式的にかけますので、これを(\ref{eq:intalongsemicirclearoundpole})式に代入すると、$\theta$が$\pi$から$0$まで変化することに注意して、
\begin{align} I &= \int_{\pi}^{0} \frac{1}{r^ne^{in\theta}} ire^{i\theta}d\theta \nonumber \cr &= \int_{\pi}^{0} \frac{ie^{i(1-n)\theta}}{r^{n-1}} d\theta \nonumber \cr &= \left[ \frac{e^{i(1-n)\theta}}{(1-n)r^{n-1}} \right]_{\pi}^{0} \nonumber \cr &= \frac{1-e^{i(1-n)\pi}}{(1-n)r^{n-1}} \label{eq:resultofintalongsemicirclearoundpole} \end{align} となります。
簡単に考察。
(\ref{eq:resultofintalongsemicirclearoundpole})式のように計算はできますが、分母に$r$ が残るため、$n \gt 1$のときに$r \to 0$ とすると、分子が0でない場合には$I \to \infty$ に発散してしまいます。 分子が0となるのはnが1より大きい奇数のときだけであり、この場合に限り、周回積分の半分の値となると言えることは言えます。
2で割る以前に$n \gt 1$ならば、 \begin{align} I_{C} &= \oint_{|z|=r} \frac{1}{z^n}dz = 0 \end{align} なんですけどね。(´・ω・`)
よって、$f(z) = \displaystyle\frac{f_0(z)}{z^n} (n \gt 1)$みたいな関数があって、上図の$C_4$に沿った経路積分を計算するために$f_0(z)$をテイラー展開してから$z^n$で割った式の項のうち、負の偶数次の項の係数が0でなかったりすると、そこで試合終了となってしまいます。
スポンサーリンク
まとめ
この記事では極のまわりを完全には回らない複素積分を計算してみました。
お寿司🍣と同様に、回る方は手っ取り早く結果が出て気軽に使えるのに比べて、この記事で扱ったような回らない方は気軽ではない反面、もしかすると味わい深いのかもしれません。
おあとがよろしいようで。
この記事は以上です。
リンク
(sin^x/x)^nの(-∞,∞)における広義積分を計算してみた。のページに戻る | メインページ | panda大学習帳 | 第三倉庫(仮) | 用語集📒 | 本サイトについて | プライバシーポリシー
スポンサーリンク
