標準正規分布に従う2個の確率変数の積が負になる場合に、その確率変数が従う確率密度関数を計算してみた。

このページはこちらの記事の続きのようなものになります。

標準正規分布に従う独立な2個の確率変数の積が正になる場合の確率密度関数の計算についてはこちらの記事で書きましたが、この記事では、2個の確率変数の積が負になる場合の確率密度関数の計算方法について書きます。

サクサクと計算します。

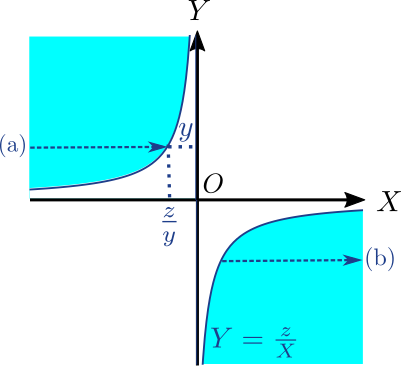
標準正規分布に従う独立な2個の確率変数$X,Y$の積$Z=XY$が負になる場合の積分の範囲を$XY$平面上に図示すると、下図の水色の領域になります(境界も含みます)。

積分の範囲

$Z$のとる値が$z(<0)$以下となる確率は、$z>0$の場合と同様に(\ref{eq:Pxy})式で表されます。

\begin{align} P\{ XY\le z \} &= P\{ XY\le z,Y \ge 0 \} + P\{ XY\le z, Y \le 0\}\label{eq:Pxy} \end{align}

ここからは$Y$の符号により場合分けして考えます。なお、$z>0$の場合と同様に計算できる部分については計算途中の過程を大幅に省略しています。あらかじめご了承ください。

$Y$が正の場合

(\ref{eq:Pxy})式の右辺の第1項は(\ref{eq:Pxypositive})式のように計算できます。上図の(a)の向きに最初に積分するイメージになります。なお、(\ref{eq:Pxypositive})式の右辺では$Y$を$y$と書き換えています。

\begin{align} P \{ XY\le z,Y \ge 0 \} &= \frac{1}{2\pi}\int^{\infty}_{0} e^{-\frac{y^2}{2}}dy\int^{\frac{z}{y}}_{-\infty}e^{-\frac{x^2}{2}}dx \label{eq:Pxypositive} \end{align}

(\ref{eq:Pxypositive})式をよーく見ると$z>0$の場合とまったく同じ式(こちらの記事の(2)式参照。)ですので、(\ref{eq:Pxypositive})式の右辺は、

\begin{align} P\{XY\le z,Y \ge 0\} &= \frac{1}{2\pi}\int^{\infty}_{0}e^{-\frac{y^2}{2}}dy\int^{z}_{-\infty}\frac{1}{y}e^{-\frac{u^2}{2y^2}}du \label{eq:Pxypositivefirst} \end{align} と計算できます。

$Y$が負の場合

次に、(\ref{eq:Pxy})式の右辺の第2項を計算してみます。

(\ref{eq:Pxy})式の右辺の第2項は、 \begin{align} P\{XY\le z,Y \le 0\} &= \frac{1}{2\pi}\int^{0}_{-\infty}e^{-\frac{y^2}{2}}dy\int^{\infty}_{\frac{z}{y}}e^{-\frac{x^2}{2}}dx \label{eq:Pxynegative} \end{align} と計算できます。

この式もよーく見ると、$z>0$の場合とまったく同じ式(こちらの記事の(5)式参照。)ですので、(\ref{eq:Pxynegative})式の右辺は、(\ref{eq:Pxypositivefirst})式の右辺と同じ式に変形できます。

まとめてから、変数変換します。

上記の議論から、$P\{XY\le z\}$は(\ref{eq:Pxyfinal})式で表されます($u$を$x$に置き換えています)。 \begin{align} P\{XY\le z\} &= \frac{1}{\pi}\int^{\infty}_{0}e^{-\frac{y^2}{2}}dy\int^{z}_{-\infty}\frac{1}{y}e^{-\frac{x^2}{2y^2}}dx \label{eq:Pxyfinal} \end{align}

(\ref{eq:Pxyfinal})式の$x$及び$y$についての積分の順序は入れ替えることができます。そこで、積分の順序を入れ替えてから$z$で微分すると、$z$における確率密度関数$p(z)$が以下のように計算できます。 \begin{align} p(z) &= \frac{1}{\pi}\int^{\infty}_{0}\frac{e^{-\frac{y^2}{2}-\frac{z^2}{2y^2}}}{y}dy \label{eq:pzfinal} \end{align}

次に、(\ref{eq:pzfinal})式で$t=\displaystyle\frac{y^2}{2}$とおきます。すると、$\displaystyle\frac{dy}{dt}=\displaystyle\frac{1}{\sqrt{2t}}$となりますので、(\ref{eq:pandt})式のように変形できます。 \begin{align} p(z) &= \frac{1}{\pi}\int^{\infty}_{0}\frac{1}{\sqrt{2t}}e^{-2t-\frac{z^2}{4t}}\frac{1}{\sqrt{2t}}dt \nonumber \cr &= \frac{1}{2\pi}\int^{\infty}_{0}\frac{1}{t}e^{-2t-\frac{z^2}{4t}}dt\label{eq:pandt} \end{align}

…とここまで長々と計算してきましたが、ここからが$z>0$の場合と$z<0$で異なる部分になります。

$t = -\displaystyle\frac{ze^{\eta}}{2}$とおきます。(\ref{eq:pandt})式の積分区間は$[0,\infty]$ですが、$\eta$の積分区間は$[-\infty,\infty]$となることと、$\displaystyle\frac{dt}{d\eta} = -\displaystyle\frac{ze^{\eta}}{2}$であることから、 \begin{align} p(z) &= \frac{1}{2\pi}\int^{\infty}_{-\infty}\frac{1}{\displaystyle\frac{ze^{\eta}}{2}}\exp\left[2\frac{ze^{\eta}}{2}+\frac{z^2}{4\frac{ze^{\eta}}{2}}\right]\frac{ze^{\eta}}{2}d\eta \nonumber \cr &= \frac{1}{2\pi}\int^{\infty}_{-\infty}\exp\left[\frac{ze^{\eta}}{2}+\frac{z}{2e^{\eta}}\right]d\eta \nonumber \cr &= \frac{1}{2\pi}\int^{\infty}_{-\infty}\exp\left[z\frac{e^{\eta}+e^{-\eta}}{2}\right]d\eta \nonumber \cr &= \frac{1}{2\pi}\int^{\infty}_{-\infty}\exp\left[z\cosh(\eta)\right]d\eta \label{eq:expcosh} \end{align} となります。

ここで、(\ref{eq:expcosh})式の右辺の$\exp(\cdot)$の$\cdot$の部分をじーっと見ると、$z$は$\eta$に依存しない定数であり、$\cosh(\eta)$は偶関数であり、さらに$z<0$なので$z = -|z|$と書けます。

したがって、(\ref{eq:expcosh})式の右辺は、

\begin{align} p(z) &= \frac{K_0(-z)}{\pi} = \frac{1}{\pi}\int^{\infty}_{0}\exp\left[-|z|\cosh(\eta)\right]d\eta \nonumber \cr &= \frac{K_0(|z|)}{\pi} \label{eq:expcoshfinal} \end{align}

となります。なお、(\ref{eq:expcoshfinal})式で、$K_0(x)$は第2種変形Bessel関数を表します。

まとめ

ここまで、$z<0$の場合の確率密度関数について書いてきました。積分の計算はサボって計算しようとすると符号の付け忘れ等の細かい計算ミスをしてしまいがちなので、慎重に計算してみましたが、$z>0$の場合と異なるのは最後の変数変換の時の符号が反転するところだけであることがわかりました。

なお、GitHub PagesでMathJaxを使うための設定や注意点などについてはpanda大学習帳で別の記事を立てて書く予定です。

この記事は以上です。

参考文献

Adding MathJax to a GitHub Pages Jekyll Blog

リンク

panda大学習帳外伝

勝利の方程式の解き方。